E(r, t) = -  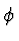 (r, t) - (r, t) -  A(r, t) A(r, t) |
|
A: Vektorpotential, erfllt die Wellengleichung |
(121) |
B(r, t) =  x A(r, t)
x A(r, t) |
|
Magnetfeld |
(122) |
 A = 0 A = 0 |
|
Coulomb-Eichung |
(123) |
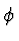 = 0
= 0 |
|
im leeren Raum |
(124) |
 (r, t) = (r, t) =  A0( A0( ) ) [expi( [expi( . .  - - t+ t+ )+c.c.] )+c.c.] |
|
 : Polarisation : Polarisation |
(125) |
P = 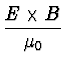 |
|
Pointingvektor = Energiefluá pro Einheitsflche
|
(126) |
H =  ( ( - q
- q )2 + q )2 + q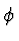 |
|
Hamilton fr geladenes Spinloses Teilchen im Feld |
(127) |
i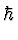   (r, t) = (r, t) = 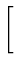  (- i (- i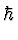  + eA)2 -
+ eA)2 - 
![$\displaystyle \left.\vphantom{{1\over 2m} (-i \hbar \nabla + e A)^2 - {Z e^2 \over 4 \pi
\varepsilon_0 r} }\right]$](img343.gif)  (r, t) (r, t) |
|
Wechselwirkung mit EM-Feld = Strung |
(128) |
 ... ...![$\displaystyle \left.\vphantom{ ... }\right]$](img345.gif) =
=  - p2 -
- p2 -  -
- 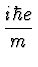  . .  +
+  A2 A2![$\displaystyle \left.\vphantom{ -p^2 - {Z e^2 \over 4 \pi
\varepsilon_0 r} - {i \hbar e \over m} \vec{A} \cdot \nabla +
{e^2 \over 2m} A^2 }\right]$](img349.gif) |
|
aus Coulombeichung! |
(129) |
H'(t)) = - 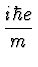  . .  |
|
Stroperator |
(130) |


 | Mba|2
| Mba|2