- Abzhlbare Orthonormalbasis
 n'| n
n'| n =
= 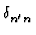
(1) - Jeder Zustandsvektor kann in dieser Basis dargestellt
werden:
| 
 =
= 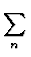
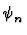 | n
| n
(2) - Die Entwicklungskoeffizienten
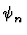 kann man als
Koordinanten von
|
kann man als
Koordinanten von
|
 auffassen, sie sind gegeben
durch:
auffassen, sie sind gegeben
durch:
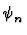 =
=  n|
n|

(3)
|
|
(4) |
|
| |
(5) |
Beispiel: Der Zeitentwicklungsoperator U(t) = e-iHt

|
|| |
(6) |
|
At| |
(7) |